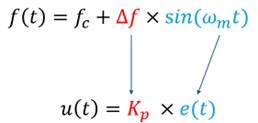Using a PID Controller to Generate Frequency Modulation (FM) Signals

Introduction

Frequency modulation (FM) and amplitude modulation (AM) signals are useful for many applications; for example, non-linear dynamics of NEMS sensors and NV ensemble-based magnetometry for quantum sensing. With the MOD option on Zurich Instruments' lock-in amplifiers, we can generate AM signals and narrow band FM signals with modulation index \(h < 0.2\). In this blog, taking the UHFLI Lock-in Amplifier as an example, we introduce a method to generate a wideband FM signal with the PID controller option available on all Zurich Instruments' lock-in amplifiers.

To understand how this works, it's important to first understand the concept of frequency modulation, which refers to the modulation of an oscillating signal \(s(t) = A\cos(ω_ct+\phi)\), the so-called carrier signal. \(A\) and  \(ω_ct+\phi\) are the amplitude and phase of the signal. In the case of frequency modulation, the frequency (\(f_c = \omega_c /2\pi\)) of this carrier signal is modulated by a sinusoidal signal with the frequency \(f_m= \omega_m/2\pi\). Thus, the instantaneous frequency of FM signal is \(f(t) = f_c + \Delta{f}*sin(ω_mt)\), where \(\Delta{f}\) is the maximum variation of the frequency around the carrier frequency. This equation of \(f(t)\) follows the same manner as the proportional term \(K_p*e(t)\) in the PID control, as shown below.

Therefore, if we feed a sinusoidal signal to the PID input \(e(t)\), we will be able to generate the instantaneous frequency of the FM signal through the PID output by applying a proportional coefficient \(K_p\).

To set up the frequency modulation with a PID controller, we exploit the advanced flexibility of LabOne, the user interface to control Zurich Instruments' lock-in amplifiers. Here are the modules you will need: 

• PID option
• MF option (recommended)